I used to work in plasma physics. A plasma is just a gas -- say, simple hydrogen gas -- which has been heated up to the point where the atoms come apart. At high enough temperature, the energy binding an electron to the nucleus (a single proton in this case) to form an atom is overwhelmed by the kinetic energy in collisions. The result is a hot gas of charged electrons and nuclei (protons), in which the particles, being charged, now interact over extended distances, unlike in normal gases where particles only interact when they undergo direct collisions.
These longer range interactions make plasmas behave very differently from ordinary gases, whether the plasma is in the Sun or the Earth's upper atmosphere, in a nuclear reactor, the interstellar medium, or in a particle beam racing around an accelerator. The basic properties of a plasma in equilibrium -- say, held at a fixed temperature in a glass tube -- were worked out (at least approximately) long ago, although the physics is still so rich that many subtle mysteries remain.
As soon as you do anything interesting with a plasma, taking it a little out of equilibrium, things get infinitely more complicated. Natural plasmas not held in fixed and unchanging conditions do all kinds of surprising things -- mostly involving natural instabilities driven by positive feed backs.
I think this example of what happens in a very simple system should give us some hints about how we should go about studying far more complicated things like markets and economies.
A good example of plasma surprises comes from the ongoing project to harness energy from nuclear fusion. The recipe for success seems simple: heat up some hydrogen gas to enormous temperatures and you create conditions in which colliding hydrogen nuclei will fuse together to form heavier nuclei. As an aside, you can't use ordinary hydrogen, but have it's isotopes, deuterium or tritium, the nuclei of which contain a proton and either one or two neutrons. These things can fuse together into unstable nuclei, which decay, ultimately creating nuclei of the stable element helium, with two neutrons and two protons. Lots of energy is given off in the process, so the reaction can be self-sustaining.
Lots of fusion requires nothing but high temperature (so the collisions are very energetic) and high density (so there are lots of collisions). So you put a mixture of deuterium and tritium into a container, heat it up and compress it, and there you go -- cheap, virtually inexhaustible energy. The only problem -- and it's a very big problem -- is making the damned plasma behave itself as you try to do this.
One of the principal routes for pursuing fusion energy is so-called Inertial Confinement Fusion (ICF). The idea is to take a tiny pellet which has a mixture of deuterium and tritium in it, and blast it from all sides with extremely high intensity x-rays. This violent bath vaporizes the pellet surface, producing plasma that explodes outward, compressing the rest of the pellet inward and creating extreme densities and temperatures. Through further mechanisms -- colliding shock waves and such -- you hope to get a fair number of nuclei colliding with sufficient energy to undergo fusion, giving off still more energy.
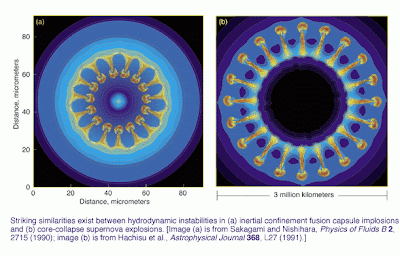
But it doesn't work, at least not yet, because of plasma misbehavior. The figure below illustrates the typical problem -- as the dense hot plasma rushes inwards, the spherical symmetry inevitably gets spoiled by growing ripples. These are caused mostly by the so-called Rayleigh-Taylor instability that happens whenever a lighter fluid pushes on a heavier fluid. As the waves get bigger, this first instability causes secondary instabilities of other kinds. In the figure below, the initially nice symmetry gets hopelessly ruined and different parts of the compressing system get mixed together, which undermines the process that would have given high temperature and density. Interestingly, what happens in inertial confinement fusion during implosion (left image) is very close to what happens during a supernovae explosion (right image).
The second figure below shows how one wave growing from the Rayleigh-Taylor instability soon creates a cascade of other instabilities, and the situation becomes infinitely complex very quickly through the interaction of several instabilities.
Remember, this all comes out of nothing but a system of electrons and positive nuclei compressed and heated in a spherically symmetric situation. The system in fact is remarkably simple. But natural instabilities -- mechanisms that make small differences and imbalances grow into much larger ones -- make it's behaviour anything but simple. Fifty years of intense research and engineering on inertial confinement fusion still hasn't managed to tame these problems. The plasma always finds another way to do something surprising that no one predicted.
Because of these instabilities, there's not a lot that is simple in plasma physics. Systems that are conceptually simple -- a beam of one single kind of particle flying around a circular ring in an accelerator -- can go unstable in hundreds of ways. There used to be a book (now out of print, I think) called the Handbook of Plasma Instabilities, which tried to list and describe all the stereotypical ways that a plasma in different simple situations will do something surprising and unexpected because of positive feed backs. It was about 800 pages long. Every entry testified to some situation in the past in which physicists or engineers had tried to do something with a plasma, only to find that it refused to go along -- its stable behaviour giving way, often explosively, to some wobbling or mixing or unexpected heating and so on.
The names of these instabilities refer crudely to what happened, why it happened or who first explained what happened. The list (wikipedia gives a brief one here) starts with the Beam acoustic instability, Bump-in-tail instability, Buneman instability, Cerenkov instability, Chute instability, Coalescence instability, Collapse instability, Counter-streaming instability, etc, continues through the Fan instability, Filamentation instability and Firehose instability leads up to the Oscillating two stream instability, Pair instability, Parker instability and Peratt instability, and finishes with the Two-stream instability, Weak beam instability, Weibel instability and Z-pinch instability. That's just a sample.
All the instabilities mentioned above illustrate how a really simple thing -- some charged particles held in a bottle -- has an extraordinarily rich set of dynamics because of natural non-linearities and interactions and the positive feed backs to which they lead. In the case of plasma, we know the laws of behaviour for the individual particles with perfect accuracy (Newtonian mechanics with corrections from quantum mechanics when necessary). Even so, these systems still surprise as as much as they do what we expect.
Now, let's think about finance and economics. Here we're dealing in general with systems made of people driven by thoughts and emotions and interactions with other people. We surely don't know with perfection the laws of behavior of these people -- we have a few crude rules offering guidance to how they sometimes behave or might behave. Humans being among the most complex things in the universe, we should surely expect these systems to present a much richer set of possibilities than a simple plasma. Indeed, we know that markets and other economic systems, historically, have routinely acted in surprising ways and caused crises of many different kinds. Even so, theories in economics and finance have until very recently been centered almost entirely on the study of equilibrium systems, with positive feed backs rarely being considered.
This shortcoming is one of the principal motivations for lots of recent work by physicists and others aimed at modeling and understanding natural instabilities in economic systems. The list of instabilities likely to be found will probably be a lot longer than the list in plasma physics. In my talk in Durham, I'm going to take a stab at making a similar (crude and very incomplete) list of some economic and financial instabilities. As in plasma physics, we should find instabilities acting on many timescales -- from milliseconds up to years. We should find some that act through fairly mechanical processes (laws which compel certain behaviours), and others working on the basis of natural human psychological and decision making tendencies (learning, speculation and so forth). We'll find some that take off through the actions of only a few parties (hedge funds, for example, during the "Quant Meltdown" of August 2007) and others driven by large-scale network effects.
I haven't finalized my talk yet, but I intend to describe very briefly some recent work on a number of these kinds of instabilities (perhaps they should be called classes of instabilities, as many distinct situations may fall into classes of quite similar behaviour). My initial list:
1. Expectations instabilities -- these include market rallies or crashes driven by the interaction of chartists versus fundamentalist investors, or more general models of markets or economies in which people have heterogenous expectations. A fascinating example (of which there are quite a few) is this paper by Brock and Hommes from 1997 in which almost rational individuals acting adaptively in a simple market lead to natural instabilities and a true strange attractor (dynamical chaos) in the market.
2. Leveraged/correlated strategies instabilities -- the sub-prime fiasco is probably a good example of this, as so many banks were heavily leveraged and invested in CDOs and other assets ultimately backed by the mortgage market. But a more specific and perhaps simpler example to analyse is the Quant Meltdown of August 2007, during which a number of hedge funds went bust in two explosive episodes lasting only a few hours. I'll describe a simple and beautiful model (in this paper by Farmer, Geanakoplos and Thurner) suggesting a natural instability which puts a market in a metastable state in which explosive collapse is certain in the long run, yet hard to predict in its timing as the end is triggered by a random spark.
3. Hedging instabilities -- several recent papers (here and here, for example) document how adding more hedging instruments to a market, which traditional theories suggest should make markets more complete and effficient, actually makes them more unstable.
4. Trend following/relative strategy instabilities -- in a recent post I reviewed ongoing events in markets driven by high-frequency trading which suggest the action of some very unstable natural dynamics. These dynamics, still unknown in detail as yet, were probably behind the Flash Crash of 6 May, 2010, as well as a number of more recent similar events in which single stocks have plummeted to a few pennies in a matter of minutes before recovering. One of the most interesting analyses I've seen is this one by computer scientist Michael Kearns and colleagues, who analysed data from HFTs and found the signature of dynamical chaos (positive Lyapunoc exponents) in the dynamics of the order book (the book in which actors place market orders or limit orders to facilitate trades). The trouble seems to be caused by algorithms which use "relative strategies" -- taking action not on the basis of some fundamental view of prices, but reacting to recent price movements.
5. Diversification instabilities -- I'll also explore briefly the conclusions of this provocative paper which shows how an increasing density of risk sharing between banks in a network, naively believed to decrease overall systemic risk, can actually increase risk to the entire system. A network can become dangerously over-dense.
I'll also make a few stray comments on some other instabilities too -- the "loss of trust" instability, the "gaming" instability, the "looting" instability and the "this time is different" instability.
But my point overall isn't to argue that this list is anything but arbitrary. The more important point is to argue that making a list of this sort, and understanding the spectrum of natural market instabilities, ought to be a main focus of the science of finance and economics. The long-standing fixation on equilibrium analyses in economics effectively rule out of existence precisely the events and processes of greatest interest.
